CYLINDER BUCKLING CALCULATIONS

hydraulic cylinders selection mostly depend on the critical buckling strength and bending strength of the cylinder apart from the other criteria like bore diameter,rod diameter and stroke length.

Buckling is a kind of failure where the cylinder fails under axial compressive load. In science, buckling is a mathematical instability, leading to a failure mode. Theoretically, buckling is caused by a bifurcation in the solution to the equations of static equilibrium. At a certain stage under an increasing load, further load is able to be sustained in one of two states of equilibrium: an undeformed state or a laterally-deformed state.

 In practice, buckling is characterized by a sudden failure of a structural member subjected to high compressive stress, where the actual compressive stress at the point of failure is less than the ultimate compressive stresses that the material is capable of withstanding.

while calculating buckling we normally use the most conventional formula of mathematician Leonhard Euler.He derived a formula that gives the maximum axial load that a long, slender, ideal column can carry without buckling. 

An ideal column is one that is perfectly straight, homogeneous, and free from initial stress. The maximum load, sometimes called the critical load, causes the column to be in a state of unstable equilibrium; that is, the introduction of the slightest lateral force will cause the column to fail by buckling. The formula derived by Euler for columns with no consideration for lateral forces is given below. However, if lateral forces are taken into consideration the value of critical load remains approximately the same.

EULER'S FORMULA :- 

where

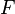= maximum or critical force (vertical load on column),

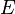= modulus of elasticity,

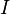  = area moment of inertia,

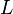= unsupported length of column,

= column effective length factor, whose value depends on the conditions of end support of the column, as follows.

For both ends pinned (hinged, free to rotate), = 1.0.

For both ends fixed, = 0.50.

For one end fixed and the other end pinned, = 0.699....

For one end fixed and the other end free to move laterally, = 2.0.

is the effective length of the column.

 Examination of this formula reveals the following interesting facts with regard to the load-bearing ability of slender columns.

1. Elasticity and not compressive strength of the materials of the column determines the critical load.
2. The critical load is directly proportional to the second moment of area of the cross section.
3. The boundary conditions have a considerable effect on the critical load of slender columns. The boundary conditions determine the mode of bending and the distance between inflection points on the deflected column. The closer together the inflection points are, the higher the resulting capacity of the column.

 The strength of a column may therefore be increased by distributing the material so as to increase the moment of inertia. This can be done without increasing the weight of the column by distributing the material as far from the principal axis of the cross section as possible, while keeping the material thick enough to prevent local buckling. This bears out the well-known fact that a tubular section is much more efficient than a solid section for column service.
Another bit of information that may be gleaned from this equation is the effect of length on critical load. For a given size column, doubling the unsupported length quarters the allowable load. The restraint offered by the end connections of a column also affects the critical load. If the connections are perfectly rigid, the critical load will be four times that for a similar column where there is no resistance to rotation (hinged at the ends).
Since the moment of inertia of a surface is its area multiplied by the square of a length called the radius of gyration, the above formula may be rearranged as follows. Using the Euler formula for hinged ends, and substituting A·r² for I, the following formula results.

where is the allowable stress of the column, and is the slenderness ratio.

Since structural columns are commonly of intermediate length, and it is impossible to obtain an ideal column, the Euler formula on its own has little practical application for ordinary design. Issues that cause deviation from the pure Euler strut behaviour include imperfections in geometry in combination with plasticity/non-linear stress strain behaviour of the column's material. Consequently, a number of empirical column formulae have been developed to agree with test data, all of which embody the slenderness ratio. For design, appropriate safety factors are introduced into these formulae. One such formula is the Perry Robertson formula which estimates of the critical buckling load based on an initial (small) curvature. The Rankine Gordon formula is also based on experimental results and suggests that a strut will buckle at a load Fmax given by:

where Fe is the Euler maximum load and Fc is the maximum compressive load. This formula typically produces a conservative estimate of Fmax.

Normally for factor of safety for linear buckling is taken more than 3.5.


hope this helps the needful..
If any query about this topic please comment..